A comment on my previous blog entry (by qraal) pointed out something that is obvious to those familiar with MiHsC, but needs to be more widely known: MiHsC does not just predict galaxy rotation like other models (eg: MoND and MOG) but, as I've shown in my papers, it can explain many other eclectic (varied) anomalies that have been seen, from cosmological scales right down to the lab scale (emdrive).
As an introduction for those who are new to this blog. Unruh radiation is like Hawking radiation but is predicted to be seen only by accelerating objects. Its wavelength gets longer as accelerations reduce. MiHsC says that the long-taken-for-granted property of inertial mass is caused by the relativistic Rindler horizon that opens up behind objects when they accelerate. This horizon then damps the Unruh waves on that side but not in front, thus making a radiation pressure that resists the original acceleration and causes humans to say 'that's inertial mass'. This force is also weakened when objects have tiny accelerations because the Unruh waves get long enough to be damped by the spherically symmetric Hubble horizon leading to a new prediction: a weakening of inertia at very low accelerations. MiHsC is encapsulated by the equation below, which is an approximation to the real process of Unruh waves being deselected by horizons
As an introduction for those who are new to this blog. Unruh radiation is like Hawking radiation but is predicted to be seen only by accelerating objects. Its wavelength gets longer as accelerations reduce. MiHsC says that the long-taken-for-granted property of inertial mass is caused by the relativistic Rindler horizon that opens up behind objects when they accelerate. This horizon then damps the Unruh waves on that side but not in front, thus making a radiation pressure that resists the original acceleration and causes humans to say 'that's inertial mass'. This force is also weakened when objects have tiny accelerations because the Unruh waves get long enough to be damped by the spherically symmetric Hubble horizon leading to a new prediction: a weakening of inertia at very low accelerations. MiHsC is encapsulated by the equation below, which is an approximation to the real process of Unruh waves being deselected by horizons
On cosmic scales MiHsC correctly predicts the recently observed cosmic acceleration. This drops straight out when you put the above formula for mi into Newton's 2nd law and gravity law. You can try it yourself! At the same scale MiHsC predicts the recently-observed unexpected smoothness of patterns in the Cosmic Microwave Background (the so called low-L CMB anomaly). The Hubble horizon is damping long waves.
MiHsC predicts the rotation of all galaxies from tiny dwarfs, through discs to galaxy clusters, and just from the equation above, whereas MoND has to be 'tuned' by parameter a0, and dark matter has to be packed-in differently for each galaxy to make the rotation curve fit general relativity. MiHsC also predicts why the oddities start when accelerations go below a particular value: the Hubble horizon then starts deselecting the long Unruh waves (see diagram below).
MiHsC predicts the Pioneer, Galileo and Ulysses anomalies, with its weakening of inertial mass at low accelerations. The Pioneer anomaly has been also explained by a complex thermal model, but the emphasis here being on complex.. I distrust complex adjustable models. MiHsC predicts the flyby anomalies, close, but not perfectly, as being due to the weakening of inertia since mutual accelerations between passing spacecraft and the spinning Earth are lower near the poles, reducing the inertia mass of the craft and by conservation of momentum (mass times speed) boosting their speed.
It predicts the anomalous effects seen by Tajmar when he spun a supercooled disc and noted that a nearby accelerometer moved slightly with the disc (with no frictional contact).
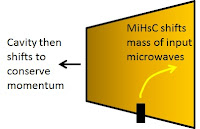
It predicts the Emdrive, a truncated metal cavity with microwaves inside, which, In MiHsC, is rather like joining a big cosmos (the wide end) which allows more Unruh waves (more inertia) to a small cosmos (allows fewer waves, less inertia) so that objects, microwave photons in this case, going from the small end to the big end gain mass (ie: the mass shifts rightwards, see diagram) so to conserve momentum (mass x speed) the cavity has to go the other way, as it does. The numbers agree with the data quite well.
This list represents successes from a cosmic scale of 10^26 metres, right down to the lab scale of a 0.1m! I'm now working on the proton radius anomaly which may give me another 10 orders of magnitude of scale. I should say also, that MiHsC reduces to the standard model for high accelerations (in the equation above hen a is huge then mi = mg, the famous equivalence principle) so it is not contradicted by any empirical data.
MiHsC can also be called quantised inertia, which is a more accessible name. Another possible name is 'horizon mechanics', which was suggested recently by someone who's read my book: John Michael Dorman. More theoretically, it is another step consistent with the history of science, which has always progressed by debunking invisible quantities, like the Greek gods (Thales), epicycles (Newton), the aether (FitzGerald, Einstein). Now we can jettison dark matter (well, most of it). MiHsC also links together relativity and quantum mechanics in a natural way.
Mathematically, MiHsC is not complete, instead of the equation above, it ideally needs a formula to describe exactly how Unruh waves are allowed or disallowed by horizons of a complex shape, and then how the remaining Unruh waves push the object around. There lots of scope for mathematicians here..
Experimentally, the best way to prove MiHsC would be to try and accelerate an object so much that the Unruh waves it is assumed to see, become small enough (they're usually light years long) to be interfered with by our technology. For example if you set up a spinning disc or resonate light within a cavity, and then block the Unruh waves on one side only, MiHsC predicts the object should move towards the blockage.


10 comments:
But doesn't that formula not only reduce the inertial mass, but also allows it to be negative when a <= ~1.8e-9 m/s^2? So, anything approaching the sun beyond ca. 1800 AU should react to that acceleration by being repelled!?
The interaction between the MiHsC formula for inertia and dynamics means the inertial mass can never become negative. As the inertial mass (mi) tends to zero, it becomes easier to accelerate the object with the same external force, so acceleration increases again and so the inertial mass never becomes negative. A minimum acceleration is the result - equal to the observed cosmic acceleration.
@Mike: How behaves MiHsC at schwarzschild radius?
For a start, MiHsC increases the Schwarzschild radius, rs. In the usual calculation you assume rs is where KE=PE, so mc^2/2=GMm/r and this gives a radius rs=2GM/c^2. Replacing the m on the left hand side with MiHsC's inertial mass gives rs=2GM/c^2 * (1/(1-2c^2/aTheta)).
MiHsC also predicts a maximum black hole mass, which agrees with the visible mass of the cosmos, see my paper: http://www.mdpi.com/2075-4434/2/1/81
I have heard of arguments against MiHsC, but strangely I did not understand really if it is working. It is probably a good occasion to precise.
The question is about the symmetry of accelerated referential.
Imagine one body A is fixed in one referential RA, and another body B is accelerating.
what MiHsC says is that from A/RA point of view, inertia of B relative to any quantum interaction is caused by Unruhwave, and damped by rindler horizon, but which Unruh waves and which horizon ?
since A is fixed the horizon is infinite. anyway who cares it is not accelerated relative to RA.
This mean that MiHsC, from RA, consider the Rindler horizon linked to B relative to RA, and the unruh waves cause by B acceleration, to justify that from RA/A B suffering from interactions that A see, does not accelerate infinitely, but shows an apparent inertia...
this is complex but meaningful.
what is strange is that from RA, there is no Unruh waves, no Rindler horizon, but that A from RA when interpreting the laws of physics for B have to project "à la Actor's Studio" into B shoes.
it is even strange as if you consider from RB, in B shoes, there is no Unruh waves, Rindler horizon for B, ... and that way, you consider A suffers from unruhwaves and Rindler's horizon...
I missed something.
Dear Alain,
Good question. What is missing is that you cannot say that A is fixed and B is accelerating or vice versa, since there's no absolute space. Only acceleration relative to other bodies is meaningful. I tried to explain it here:
http://physicsfromtheedge.blogspot.co.uk/2015/09/a-tale-of-two-bodies.html
Inertial forces can become quite large. I find it counterintuitive that these can be caused by radiation pressure, and yet we can't detect this radiation. Can you give me a handle on this?
A detailed derivation is in my 2013 paper in EPL, see below, but here's a quick version I've just scribbled.. Imagine a particle of Planck length (l) suddenly with acceleration a. The wavelength of Unruh radiation it alone sees, L, is
L=8c^2/a.
We know that E=hc/L so
E=ha/8c
This is the Unruh energy field seen only by the accelerating particle. The waves are typically light years long for any reasonable acceleration so we can't detect them with present technology. MiHsC says that in the space the particle is accelerating away from, a relativistic horizon forms which damps this energy. So the energy density in front is E=ha/8c and behind it is E=0. The force, from the gradient across the particle of length l is then
F=dE/dx = ha/8cl = (h/8cl) x a
This is Newton's 2nd law F=ma, for which m=h/8cl = 1.7x10^-8 kg. This is close to the Planck mass 2.2x10^-8 kg as expected for a Planck length particle (not quite right due to the crudity of this derivation).
The full derivation was published as McCulloch, 2013, EPL, 101, 59001 (https://arxiv.org/abs/1302.2775) and some errors were ironed out in Gine and McCulloch, 2016, MPL-A, 31, 17, 1650107.
Here is a new paper with null results on the search for dark matter.
http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.117.121303
Wow; thanks for that. So the energy gradient IS tiny, but division by the Planck length brings it back to a macroscopic scale...
Presumably this then predicts high weirdness whenever the particles start to get nonlocal: superconductors, superfluids, Bose-Einstein condensates...?
Post a Comment